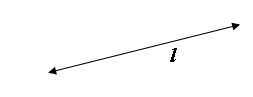Unidad I. Ángulos y triángulos
A. Encuadre
B. Objetivo de la Unidad I
C. Estrategias de Aprendizaje
D. Evaluación Diagnóstica
E. Descripción del Contenido de la Unidad I “Ángulos y Triángulos”
La Unidad 1, correspondiente al eje de Geometría Euclidiana, contemplan las etapas de exploración, deducción y aplicación, mismas que darán un soporte metodológico al programa, ya que con el estudio de las construcciones geométricas básicas, se pretende que el estudiante explore, observe patrones de comportamiento, conjeture y comience a argumentar sus conclusiones, mientras que en los temas de Congruencia y Semejanza, a partir del conocimiento básico de estos conceptos, se introduce al estudiante al aspecto deductivo y a la comprensión de las argumentaciones (demostraciones). Al final de cada unidad se da paso a combinar diversos conceptos y resultados geométricos en aplicaciones teóricas y prácticas.
B. OBJETIVOS DE LA UNIDAD I
.
GENERAL
El estudiante:
Resolverá problemas geométricos de tipo teórico o práctico de distintos ámbitos, mediante la aplicación de técnicas de medición de ángulos en el plano y su clasificación, así como las correspondientes a la medición de triángulos utilizando razonamientos analógicos y deductivos para recuperar los conceptos de semejanza y congruencia, en un ambiente escolar que favorezca el desarrollo de actitudes de responsabilidad, iniciativa y colaboración hacia el entorno en el que se desenvuelve
ESPECÍFICOS:
El estudiante:
1.1. Resolverá problemas teóricos o prácticos relacionados con ángulos en el plano, mediante la identificación, clasificación y medición de los mismos.
1.2. Resolverá problemas de triángulos de tipo teórico y prácticos aplicando los conceptos, técnicas y procedimientos relativos a los triángulos y sus propiedades geométricas, la semejanza y congruencia y el Teorema de Pitágoras.
a) El estudiante resolverá un examen diagnostico que indique el nivel de aprendizaje que tiene en ese momento y los temas que tendrá que reforzar para iniciar este curso.
b) El estudiante leerá el material, analizará y resolverá los ejemplos con los que cuenta.
c) Al final de la unidad el estudiante mandará al asesor la serie los ejercicios y actividades complementarias contenidas en este material para su evaluación.
d) Se le propone al estudiante ir verificando la solución de los ejercicios propuestos en la parte de “solución a los ejercicios propuestos”
INDICACIONES:
Para cada una de las preguntas que se te plantean enseguida selecciona la respuesta que te parezca correcta:
1. Una línea recta es:
a) La línea más corta entre dos puntos. b) La distancia recorrida de un punto a otro.
b) El radio de una circunferencia. c) El vector que va desde un punto a otro.
2. Dos líneas paralelas son aquellas que:
a) Se cruzan entre sí. b) Se cruzan entre sí a en un ángulo de 90°
c) La distancia entre ellas es constante. d) Si están en un mismo plano nunca se juntan.
3. La apertura entre dos líneas que se cruzan se llama:
a) Radián b) Arco de circunferencia.
c) Grado d) Angulo.
4. Un triángulo es:
a) Una figura plana b) Un polígono de 4 lados
c) Un polígono plano con 5 ángulos d) un polígono de 3 lados
5. Un ángulo se mide en:
a) Radios b) Radianes
c) Grados Centígrados d) Grados.
6. Todo triángulo tiene:
a) Tres ángulos y uno de ellos recto b) Tres ángulos
c) Tres lados d) Todos sus lados iguales.
7. El teorema de Pitágoras se utiliza en:
a) Triángulos rectángulos. b) El cálculo del radio de una circunferencia.
c) Todo tipo de triángulos d) Cálculo del área de un círculo.
8. La suma de los ángulos de un triángulo es:
a) 90° b) Mas de 180°
b) 360° d) 180°
E. DESARROLLO DEL CONTENIDO DE LA UNIDAD I “ÁNGULOS Y TRIÁNGULOS”
1.1.2. Clasificación
• Por sus medidas
- Llano
- Agudo
- Obtuso
- De una vuelta
• Por la posición de sus lados
• Opuestos por el vértice
- Adyacentes
• Por la suma de sus medidas
- Suplementarios
- Complementarios
1.1.3. Medición de ángulos en el sistema sexagesimal
1.1.4. Ángulos formados por dos rectas paralelas y una secante
1.2.1. Definición y clasificación
• Definición
• Clasificación
- Por la longitud de sus lados
- Por la amplitud de sus ángulos
• Rectas notables
• Perímetros y áreas
• Ángulos
- Suma de ángulos interiores
- Suma de ángulos exteriores
- Suma de dos ángulos interiores
1.2.2. Congruencia
1.2.3. Semejanza
1.2.4. Teorema de Pitágoras
1.3. Verificación de los ejercicios de la Unidad I
INTRODUCCION
La geometría es una parte de las matemáticas que nos permite el estudio de diferentes tipos de figuras y sus propiedades. Se han usado sus estudios para múltiples mediciones de nuestro entorno, de la naturaleza, del hombre, por ejemplo para las mediciones de la tierra misma. El inicio de la geometría se remonta a los principios del hombre, cuando este tuvo, por ejemplo, la necesidad de medir sus tierras. Los egipcios y babilonios encontraron múltiples formas para determinar el área de las superficies. Los matemáticos de la India también contribuyeron al crecimiento de la Geometría; incluso se dice que sentaron las bases para lo que se conoce como el teorema de Pitágoras. Los griegos participaron igualmente y con Euclides, quien coleccionó el conocimiento de esos tiempos (330 a.c.), logró darle una forma sistemática a la geometría y con ello aprovechamiento lógico basado en la deducción y el razonamiento. Desde estos tiempos, la geometría, es sistemática y para su estudio se vale de propiedades y reglas. En esta primer parte se estudiaran conceptos tales como línea, ángulo, triangulo, cuadrilátero, círculos y sus propiedades.
Introducción. En gran parte del curso nos estaremos refiriendo al “plano”, que de manera simple, diremos que es una superficie sin torceduras, hendiduras o salientes (aunque se rugosa), tal como tu mesa o tu escritorio en donde comes o estudias, o como el piso de tu sala. Sobre este plano puedes trazar una línea recta, puedes localizar un punto, líneas paralelas, por ejemplo; conceptos que seguramente has visto previamente a este curso y que sin embargo nos permitimos hablar brevemente de ellos en seguida:
| Punto. En muchas ocasiones, los distintos autores, al hablar del concepto “punto”, se refieren a la huella que sobre un papel hace la punta de un lapicero, al presionar este sobre el papel. Puedes intentarlo con distintos lapiceros, de 0.5mm, o de 0.7mm por ejemplo, y te darás cuenta que “el grosor” de esa huella es distinto; claro pues “el balín” del lapicero tiene esos distintos diámetros. Seguramente has escuchado que un “punto”, como se maneja en geometría, no tiene dimensiones, es decir, no tiene diámetro. En el ambiente de la geometría, en este curso, manejaremos la idea de “punto” algo así como la huella del lapicero sin que reparemos en pensar qué diámetro tiene esta huella. Frecuentemente se utilizan las letras mayúsculas, A, B, C, etc. para nombrar a un punto | 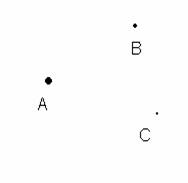 |
Línea . Si en la figura anterior tomamos únicamente los puntos A y B, y con la ayuda de una regla trazas una “raya“ que se extienda por ambos lados, tanto de A como de B, y le llamaremos simplemente “línea”. En geometría si una línea es representada por una flecha, en uno o los dos extremos, estaremos refiriéndonos a una “línea infinita “ , es decir una línea que se extiende infinitamente. Para referirse, nombrar, a un línea lo haremos bajo los siguientes casos:
• Usaremos las letras l, m, n , letras cursivas minúsculas, para representar a una “línea infinita”.
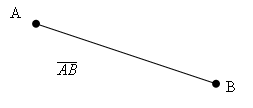
• Cuando tenga que referirse a un “segmento” de línea definido por dos puntos, A y B, lo haremos mediante la unión de las dos letras “AB” . Algunos autores lo representan como
|
|
Plano. Una idea simple de lo que es un plano, lo decíamos, es la idea del piso o el techo de tu casa. Un plano, en geometría, es esa superficie sin curvaturas o retorcimientos, sin hendiduras o salientes, la mesa de trabajo, la hoja de tu cuaderno. Una pelota, es una superficie lisa, no lo confundamos, pero no la consideraremos mas que un superficie curva. De manera similar, al concepto de línea infinita, la geometría también maneja el concepto de “plano infinito”, como una superficie plana de dimensiones infinitas; se deduce el concepto “segmento planar”
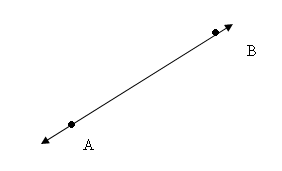
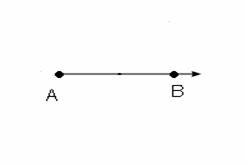
Rayo. Si ubicamos dos puntos, A y B, en un plano y trazamos una línea infinita, desde el punto A, pasando por el punto B y extendiéndose hacia el infinito, a esta línea infinita se le llama “Rayo AB”.
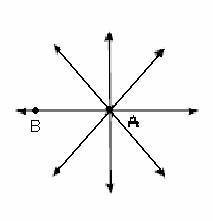
Puntos Colineales . Por un punto A en el plano podemos hacer pasar un sin número de líneas infinitas, como se muestra el la figura, todas ellas con inclinación distintas es decir con dirección diferente. En cambio, si consideramos otro punto en el plano, un punto B, separados por alguna distancia, de todas las líneas infinitas que pasen por A, sola una pasará por el punto B. Diremos entonces que “una y solo una línea puede ser traza por dos puntos dados en un plano”. De manera similar podemos hablar de tres o más puntos colineales, cuando todos ellos se encuentran sobre una misma línea.
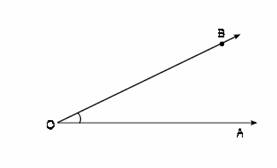
Angulo. Si marcas un punto “O” y, partiendo de él, trazas los rayos ![]()
![]() y
y ![]() , ambos no en la misma línea; a la figura que se obtiene se le llama “ ángulo”. Para nombrar o referirse a un ángulo se puede hacer de las siguientes maneras:
, ambos no en la misma línea; a la figura que se obtiene se le llama “ ángulo”. Para nombrar o referirse a un ángulo se puede hacer de las siguientes maneras: ![]() o bien
o bien ![]() o simplemente
o simplemente ![]() (observa el diagrama adjunto). Las tres formas son usuales y en este caso equivalentes.
(observa el diagrama adjunto). Las tres formas son usuales y en este caso equivalentes.
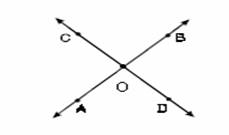
Piensa en que, cuando dos líneas se cruzan en un punto, de esta manera también se esta formando un ángulo. Date cuenta que parecen presentarse 4 figuras como aquella llamada ángulo. Más adelante se hablará más al respecto.
Unidad de medida . Una de las unidades de medida de un ángulo es la de “grados”. Para dimensionar lo que es”un grado”, pensemos en dos rayos que parten, para lados opuestos, desde un mismo punto, entonces, el ángulo que se está formando es un ángulo de 180 grados (que se representa como 180° ). Así que, si dividimos este ángulo en 180 partes iguales, tenemos que cada una de estas partes es de 1° (un grado). Este ángulo del que hablamos es llamado “Angulo Llano”.
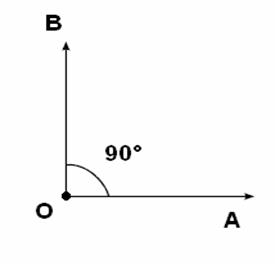
Angulo recto . Al ángulo formado por dos rayos formando un ángulo de 90°, es llamado “ángulo recto”. Observar que se trata de la mitad de un ángulo llano. Diremos que, cuando dos rayos formen un ángulo de 90°, se trata de dos “rayos perpendiculares”. En esta figura podemos decir que la línea ![]() e s perpendicular a la línea
e s perpendicular a la línea ![]() y también que
y también que ![]() es perpendicular a
es perpendicular a ![]() .
.
Angulo agudo . Todo aquel ángulo que sea menor de 90° es llamado “ángulo agudo”. En el caso de la figura, el ángulo ![]() , es un ángulo agudo.
, es un ángulo agudo.
Angulo obtuso . De manera similar se define, un ángulo mayor de 90°, como “ángulo obtuso”. En la figura tenemos que el ángulo ![]() es un ángulo obtuso.
es un ángulo obtuso.
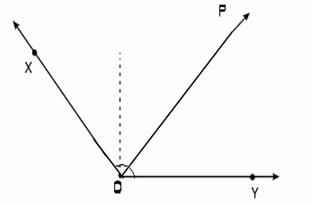
Ángulos adjuntos. Cuando dos ángulos comparten una línea, un rayo, se dice que son “ángulos adjuntos”. En esta definición no importa que estos ángulos sumen entre sí un ángulo mayor, menor o igual de 90°.
En la figura se muestra que el ángulo ![]() y el ángulo
y el ángulo ![]() tienen en común el rayo
tienen en común el rayo ![]() , por lo tanto se dice que son ángulos adjuntos. Juntos suman un ángulo menor de 90°.
, por lo tanto se dice que son ángulos adjuntos. Juntos suman un ángulo menor de 90°.
Lo mismo pasa con el ángulo ![]() y el ángulo
y el ángulo ![]() . Son ángulos adjuntos que tienen en común la línea
. Son ángulos adjuntos que tienen en común la línea ![]() y, en este caso, suman mas de 90°.
y, en este caso, suman mas de 90°.
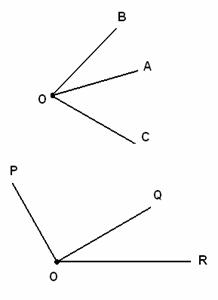
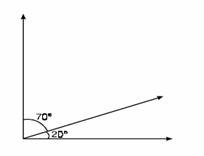
Ángulos complementarios. Cuando dos ángulos suman 90°, como en la figura, se dirá que estos son “ángulos complementarios” entre sí. Por ejemplo el ángulo de 70° es complementario del ángulo de 20°, a su vez, el ángulo de 20° también es complementario del ángulo de 70°
. 
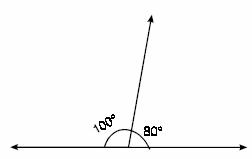
Angulos suplementarios. Cuando dos ángulos suman 180°, se dirá que estos dos ángulos son “suplementarios” entre sí. En la figura, los ángulos de 100° y 80° suman 180°. De manera semejante, al caso anterior, podemos decir que uno es suplementario del otro y viceversa.
Ángulos opuestos por el vértice. En la figura podemos ver que el ![]() y el
y el ![]() son ángulos suplementarios, porque suman 180°, pues se forman sobre la misma línea. De la misma manera el
son ángulos suplementarios, porque suman 180°, pues se forman sobre la misma línea. De la misma manera el ![]() y el
y el ![]() también son suplementarios entre sí, pues suman 180°. Entonces tenemos que los ángulos
también son suplementarios entre sí, pues suman 180°. Entonces tenemos que los ángulos ![]() y
y ![]() son iguales. Es decir:
son iguales. Es decir:
Si ![]() y
y ![]() , entonces concluimos que
, entonces concluimos que ![]() . Diremos entonces que estos ángulos “opuestos por el vértice” son iguales.
. Diremos entonces que estos ángulos “opuestos por el vértice” son iguales.
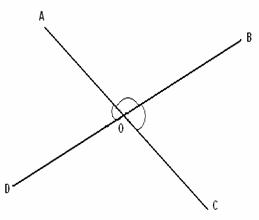
Ángulos formados por dos rectas paralelas y una secante. En la figura podemos ver dos líneas paralelas, la línea “a” y la línea “b”, cruzadas por una línea “m” llamada transversal o línea secante. Llamaremos ángulos internos a al ángulo 3,4,5 y 6, ya que quedan “atrapados, dentro” de las paralelas; los ángulos 1,2,7 y 8, serán llamados ángulos externos . Observa que, el cruce en la línea “a” es idéntico al cruce en la línea “b”, dado que estas líneas son paralelas. Así que el ángulo 1 es correspondiente con el ángulo 5, por estar en posiciones semejantes. Y lo mismo sucede para el 2 y el 6. Así que estos pares de ángulos son iguales . Tú podrás localizar pares de ángulos iguales.
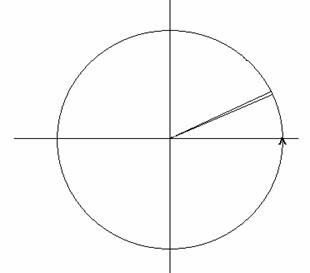
Medición de ángulos en el sistema sexagesimal. Cuando un ángulo es trazado con una “vuelta completa” estaremos hablando de un ángulo de 360°; observa como se describe una circunferencia.
Se define, como un grado , aquella parte que resulte de dividir a la circunferencia en 360 partes iguales; es decir cada una de estas partes mide un grado. Si, una de estas partes es divididita en 60 partes iguales, a cada una de estas se le dirá “un minuto ”. Por si fuera poco, si cada una de estas partes, un minuto, fueran divididas en 60 partes iguales, a estas pequeñas partes se les llama “ segundos”.
|
Resumiendo , tenemos las definiciones siguientes, en una tabla de equivalencias:
UNIDAD DE MEDIDA |
SIMBOLO |
EQUIVALENCIA |
Un grado |
1 ° |
60 minutos |
Un minuto |
1 ' |
60 segundos |
Un segundo |
1 '' |
|
EJEMPLO. Así, si medimos un ángulo y nos resulta una cantidad “no entera”, estaremos hablando de un ángulo fraccionario. Bien pudiera ser el siguiente: 34°25'17'' , que se lee como “treinta y cuatro grados con veinticinco minutos y diecisiete segundos.
Medición en el sistema decimal. Cuando un ángulo está expresado en el sistema sexagesimal (ejemplo anterior), puede expresarse en otro sistema, el decimal; en este sistema la unidad es dividida en diez partes y cada una de estas en otras diez, así podríamos hablar del ángulo 35.75°. Observa que el 0.75 es una fracción de entero equivalente a ¾ de grado. Para el ángulo 23.50°, la fracción 0.5 significa ½ grado.
Conversiones entre sexagesimal y decimal . Una gran variedad de calculadoras científicas podrían hacer la tarea de convertir un ángulo de un sistema a otro, simplemente con una combinación de teclas, esto en función del diseño de tu calculadora, es decir dependiendo de cómo trabaje esta. Para ello siempre es bueno acudir al manual de la misma. Es una pena no poder hablarles de tu calculadora en especial, desde luego, por razones obvias. Sin embargo nos permitimos presentar una manera de hacer estas conversiones mediante la herramienta de razón o proporción, llamada: regla de tres:
EJEMLO. Convertiremos el ángulo 34°25'17'' expresado en forma sexagesimal a su equivalente en forma decimal.
- Convertir 17'' a fracción de minuto:
60'' |
1' |
17'' |
( 17'')( 1' )/ 60''=0.283' |
Así es que : 17'' = 0.283' |
|
- El ángulo 34°25'17'' es ya 34°25.283' en donde la fracción 0.28 es la parte equivalente a los 17''.
- Convertimos ahora los 25.283' a una fracción de grado:
60' |
1° |
25.283' |
( 25.283' )( 1°)/ 60'=0.42° |
Así es que : 17.283' = 0.42° |
|
- El ángulo 34°25.283' es equivalente a 34.42°.
NOTA. El alumno podría asociar este procedimiento con el caso en que se haga una conversión en el sentido contrario, del sistema decimal al sistema sexagesimal. Es decir, como ejemplo, convertir 35.75 ° al sistema sexagesimal .
SECCION PARA LOS EJERCICIOS Y PROBLEMAS DEL 1.1
1.-Refiriéndonos a la figura, para las próximas preguntas selecciona la respuesta que consideres correcta:
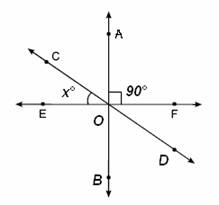
• i. Decir si los ángulos ![]() son ángulos:
son ángulos:
a) suplementarios |
b) complementarios |
c) opuestos por el vértice |
d) par de ángulos lineales |
• ii. Los ángulos ![]() son.
son.
a) suplementarios |
b) complementarios |
c) ángulos adjuntos |
d) par de ángulos lineales |
• El ángulo ![]() es igual a:
es igual a:
a) x° |
90°+ x° |
c) (180-x)° |
(90-x)° |
• Si el ángulo ![]() determina cuál es el valor del ángulo
determina cuál es el valor del ángulo ![]() .
.
a) 35° |
90°+ 65° |
c) (90+35)° |
(90-x)° |
2.- Para la figura responde a las siguientes preguntas:
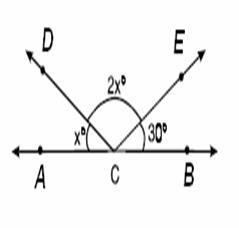
• i. Qué valor de x° hace que AB sea un ángulo llano ( de 180°)
• ii. Si el ángulo ![]() fuera de 90°, qué valor debería tener el ángulo
fuera de 90°, qué valor debería tener el ángulo ![]() .
.
3.- Determina el valor de aquel ángulo que es igual a 4 veces su suplemento.
4.- En la figura determina el valor del ángulo ![]()
. 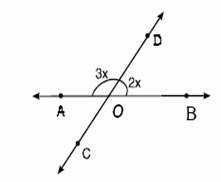
a) 36° |
b) 72° |
c)108° |
d) 144° |
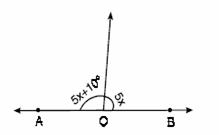
5.- En base a la figura, determina el valor de la X. Considera que el ángulo ![]() es un ángulo llano.
es un ángulo llano.
6.- Considerando a la figura, resuelve para X, si se tratara de 2x+25° y de 3x.
7.- En la figura determina el valor de los ángulos siguientes:
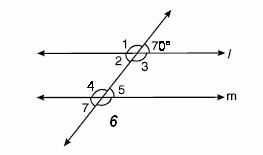
a.- 4
b.- 6
c.- 7
c.- 1
8.- Realiza las transformaciones de los ángulos siguientes según se te pida:
35°30'45'' |
Convertir a sistema decimal |
60°45'40'' |
Convertir a sistema decimal |
Convertir a sistema sexagesimal |
38.25° |
Convertir a sistema sexagesimal |
45.50° |
9.- Son dos características de la línea:
a).- Es una sucesión finita de puntos, tiene longitud y anchura.
b).-Es una sucesión finita de puntos, tiene longitud pero no anchura.
c).-Es una sucesión finita de puntos, con longitud y anchura.
d).-Es una sucesión finita de puntos, tiene longitud pero no anchura.
10.- El ángulo cuya medid es 235° es un ángulo:
a).-Perigonal
b).-Convexo
c).-Cóncavo
d).-Obtuso
11.- ¿Qué ángulo forman dos rectas perpendiculares?
a).- Agudo
b).- Recto
c).- Llano
d).- Perigonal
12.- Convertir 64°23'12'' a grados en sistema decimal.
a).- 64.380°
b).- 64.3866°
c).- 64.390°
d).- 64.3833°
13.- Convertir 237.7756° a sistema sexagesimal.
a).- 237°46.536'
b).- 237°32'46''
c).- 237°46'32''
d).- 237°46.536'
14 A partir de la figura encuentre el valor de cada ángulo. Le conviene encontrar el valor de X primeramente.
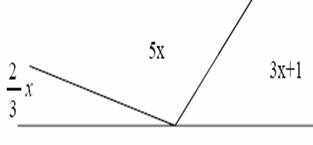
a.-68.66°, 113.32°, 2.03°
b.- 56.86°, 93.10°, 12.41°
c.- 54.76°, 88.35°, 5.27°
d.- 13.77°, 103.27°, 62.96°
15 El ángulo suplementario de 85°15'36'' es:
a.-94°44'24''
b.- 94°45'24''
c.- 4°44'24''
d.- 274°44'24''
El triángulo es simplemente una figura cerrada de tres lados. O bien un polígono de tres lados. La variedad de estos se puede clasificar atendiendo s distintos parámetros, como en sus lados.
CLASIFICACION BASADO EN SUS LADOS |
|
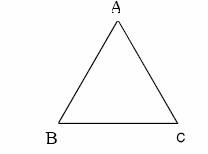
Triángulo Equilátero. Es aquel en que la longitud de sus tres lados es igual. En el ejemplo de la figura tenemos el triángulo ?ABC, en donde los lados AB, BC y CA son iguales entre sí. |
|
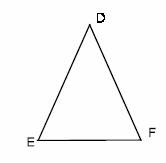
Triángulo Isósceles. Estos triángulos tienen tan solo dos lados iguales y el tercero distinto sin importar su medida. El triángulo ?DEF es isósceles y sus lados ED y FD son iguales; mientras que el lado EF es distinto a estos |
|
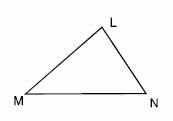
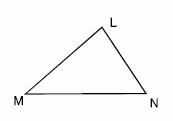
Triángulo Escaleno. Este tipo de triángulos tienen sus tres lados de distinta longitud. El triángulo ?LMN es equilátero porque sus lados LM, MN y NM, todos ellos son distintos. |
|
Nota . En los triángulos el punto de unión de cada lado se llama”vértice” y , así como ejemplo, para el triángulo escaleno, hablamos de los vértices L, M y N. Para trazar un triángulo cualquiera, una vez conocidas las longitudes de sus lados:
1.- Basta con tomar un primer segmento y trazarlo con una regla
2.- Los segmentos siguientes podrán ser trazados con un compás, esto, dándole la apertura de cada lado, para cada uno de los casos.
3.- Apoyando el compás en cada extremo y trazando una circunferencia de radio igual a la medida de cada uno de los lados.
4.- El cruce de estas circunferencias determina el tercer vértice del triángulo.
CLASIFICACION BASADA EN LOS ANGULOS . Los triángulos también se pueden clasificar, atendiendo al tamaño de sus ángulos y de la relación que estos guardan
.
CLASIFICACION BASADO EN SUS ANGULOS |
|
Triángulo Obtusángulo. Es aquel en que la longitud de uno de sus ángulos es mayor de 90°. En la figura el ángulo |
|
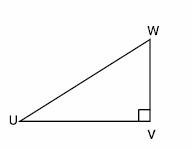
Triángulo Rectángulo. Estos triángulos tienen uno de sus ángulos exactamente de 90°, un ángulo recto. En la figura el triángulo rectángulo ?UVW, tiene un ángulo recto que es el |
|
Triángulo Acutángulo. Este tipo de triángulos tienen sus tres ángulos menores de 90°. El triángulo ?LMN es acutángulo. |
|
Nota . Para trazar un triángulo conocidos el tamaño de sus ángulos (veremos mas adelante), esta situación no es tan fácil, digamos, como en el caso del trazo de un triángulo conociendo sus tres lados. Veremos que se requiere conocer la magnitud de uno de los lados. Así es que proponemos:
- Conociendo los extremos de un lado del triángulo y con la ayuda de un transportador.
- Apoyemos éste en uno de los extremos y, con el ángulo indicado, trazar una línea que parta desde el extremo y se extienda en el plano que quieras tu triángulo.
- Repetimos el paso anterior para el segundo extremo del lado conocido.
- El cruce de estas dos líneas trazadas por los extremos será el tercer vértice de nuestro triángulo.
Suma de los ángulos interiores de un triángulo.
La suma de los ángulos de todo triángulo es de 180°. Para mostrarlo, veamos el ?ABC, encerrado en dos líneas paralelas. Analizando la figura, y recordando lo hasta ahora visto sobre ángulos, tenemos que:
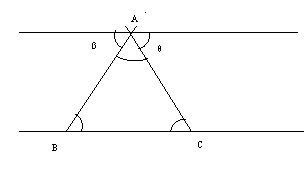
• Los pares de ángulos, B y ß, y C y ?, son iguales entre sí, por ser ángulos alternos.
• Observando la línea paralela superior vemos que ![]() por formar juntos un ángulo llano.
por formar juntos un ángulo llano.
• Dado las igualdades del primer punto concluimos que ![]() .
.
Nota. Observa que siempre puedes encerrar un triángulo, cualquiera que este sea, dentro de dos líneas paralelas; así es que este análisis es posible llevarlo a cualquier triángulo. Te invitamos a que lo intentes con un triángulo que pudieras trazar al azar.
Angulo exterior a un triángulo. En la figura, la suma de los ángulos del triángulo ?ABC es de 180°. Por otro lado en el vértice C se presenta lo siguiente:
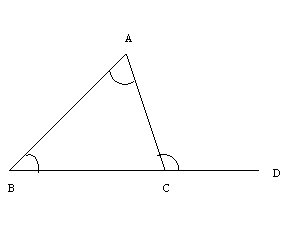
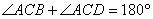 por ser ángulos suplementarios (pues forman un ángulo llano).
por ser ángulos suplementarios (pues forman un ángulo llano). - Los ángulos
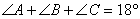 por ser los ángulos de un triángulo.
por ser los ángulos de un triángulo. - Conjugando lo anterior tenemos que los ángulos
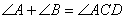 .
.
Nota. La misma situación puede decirse para cada ángulo de los otros dos vértices. Tú puedes reproducir esta demostración, por ejemplo, para el ángulo en B. Te recomendamos que lo hagas utilizando un transportador para un triángulo que traces al azar.
Reto. En el triángulo anterior, observa como en el vértice C, se dijo mas atrás, los ángulos ![]() y si observas que el ángulo
y si observas que el ángulo ![]() ,medido por debajo de la línea
,medido por debajo de la línea ![]() , es de 180°, tenemos que en el vértice C, se tiene la siguiente situación:
, es de 180°, tenemos que en el vértice C, se tiene la siguiente situación: ![]() . La pregunta a investigar es la siguiente:
. La pregunta a investigar es la siguiente:
• ¿En un triángulo cualquiera cuánto suman los ángulos trazados por fuera del triángulo, por fuera de los vértices?
Teorema de Pitágoras. El triángulo de la figura es un triángulo rectángulo, es decir con un ángulo de 90°. Los lados a y b serán llamados catetos, mientras que el tercer lado, h , el mas grande es llamado hipotenusa . El teorema de Pitágoras dice que “la suma del las áreas de los cuadros levantados sobre los catetos es igual a el área del cuadro levantado sobre su hipotenusa”. Lo anterior se puede representar mediante la siguiente ecuación matemática:
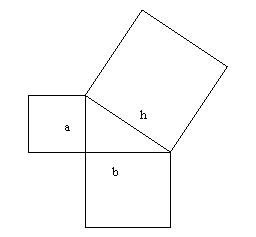
![]()
En donde ![]() son las áreas de los cuadrados mencionados.
son las áreas de los cuadrados mencionados.
Nota. La relación entre las magnitudes de los tres lados de un triángulo rectángulo puede representarse mediante este teorema de Pitágoras, de aquí su importancia. Esta relación se da mediante la expresión siguiente ![]() . Con esta expresión podemos encontrar la magnitud de la hipotenusa conociendo de antemano la magnitud de los catetos del triángulo.
. Con esta expresión podemos encontrar la magnitud de la hipotenusa conociendo de antemano la magnitud de los catetos del triángulo.
Reto. En el Internet existen una gran cantidad de paginas Web que se han estado dedicando a montar propuestas de apoyo para el aprendizaje de las matemáticas. Una de estas propuestas de aprendizaje es el uso de simulaciones dinámicas o interactivas mediante el uso del concepto apletts. Te invitamos a que:
• Visites la pagina siguiente que te presenta un tratado del teorema de Pitágoras mediante este concepto de apletts:
http://www.utc.edu/~cpmawata/geom/geom6.htm
Ejercicios del tema 1.1 y 1.2
Solución de los ejercicios de los mismos temas
Solución del examen diagnostico
1.3 Verificación de los ejercicios de la Unidad I
1.3.1. Solución del Examen Diagnóstico
- únicamente el inciso a)
- correctas c) y d)
- únicamente d)
- correctas a) y d)
- correctas b) y d)
- correctas b) y c)
- sobretodo a)
- únicamente d).
Nota . En realidad como requisito de este curso están un gran número de conocimientos del álgebra, potencia, raíz cuadrada, ecuación, igualdad, y cuestiones del álgebra básica. Se decide obviar todos estos requisitos y nos centramos en los básicos de la geometría que se cubren en secundaria. Igual, estamos pensando que en preguntas con opción múltiple, en donde se presenta una sola solución, permite que aquellos alumnos un poco familiarizados, al toparse con el primer inciso que consideren respuesta, dejen de leer los siguientes incisos. Intercalando preguntas con una y dos soluciones, los obliga a terminar de ver todos los incisos en búsqueda de mas de una solución, o bien, estaría haciendo un análisis entre las dos soluciones encontradas y esto, creemos, es sumamente provechoso. Creemos que una sola respuesta correcta es “un simple paradigma”.
1.3.2. Solución Ejercicios Y Problemas Sección 1.1
1.- soluciones.
1 d)
2 c)
3 d)
4 c)
2.- soluciones.
i. x=50°
ii. 165°
3.-d)
4.-c)
5.-a)
6.- Primer caso 17° y segundo 31°
7.- soluciones.
a.-110°
b.- 110|
c.- 70°
d.- 110°
8.- 35.5125°, 60.7611°, 38°15'0'' y 45°30'0''.
9.- b)
10.- d)
11.- b)
12.- b)
13.- c)
14.- d)
15.- a)
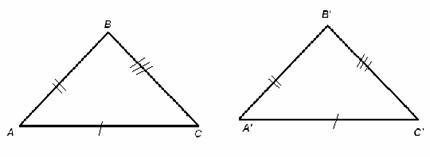
CONGRUENCIA. En esta sesión presentamos los criterios que habremos de tomar para decidir si un par de triángulos es congruente o no. Comencemos comentando que “ dos figuras planas son congruentes si una de ellas puede ser convertida en la otra por medio de movimientos, tales como: rotación, traslación, simetría con respecto a una recta. (Enciclopedia de las Matemáticas, Tomo 2 pp. 360, 1998” . En muchas ocasiones se presentan ante tus ojos dos figuras planas, por ejemplo dos triángulos, y pareciera como si fueran diferentes por tener distinta orientación en un plano cualquiera, pero resulta que estos llevados uno sobre el otro resultan empalmarse perfectamente; diremos pues, si esto sucede, que son triángulos congruentes. Una manera muy simple de decir cuándo es que dos triángulos son congruentes es cuando “estos tengan igual forma e igual tamaño”.
CRITERIOS DE CONGRUENCIA PARA TRIANGULOS. Representamos la congruencia entre dos triángulos ?ABC y ?A'B'C' como:
![]()
y los criterios para decidir sobre esta congruencia se presentan en la siguiente tabla:
CRITERIO |
DESCRIPCION |
FIGURA |
|
Tener dos lados iguales y el ángulo entre ellos también igual. |
|
|
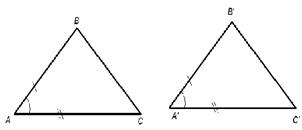
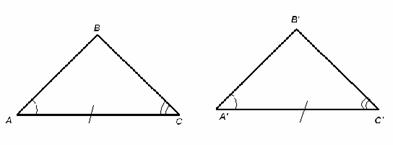
Tener dos ángulos iguales y el lado comprendido entre estoados ángulos. |
|
|
Si tienen sus tres lados iguales, es decir uno a uno deberán ser iguales. |
|
Nota. Podrías pensar en que dos triángulos que tengan sus tres ángulos iguales sean también congruentes, en comparación con el último criterio, puedes ver que esto es falso. Piensa en dos triángulos, uno dentro del otro, que tengan sus ángulos iguales, y verás que necesariamente tendrán caras paralelas… tendrán la misma forma pero no pueden tener el mismo tamaño.
Reto. Construye en una hoja blanca el caso que se te está notificando más inmediatamente atrás. Piensa en un triángulo cualquiera, trázalo y traza uno más que envuelva al primero, cuidando siempre que sus caras sean paralelas. Estos tendrán los tres ángulos iguales con sus tres lados de distinto tamaño a los del primer triangulo.
1.3.3. Solución Ejercicios Y Problemas Sección 1.2
1).- Un triángulo rectángulo tiene uno de sus lados con dimensión de 3 unidades y el otro con 4 unidades. Determina el valor de su tercer lado.
2).-Determina el valor de la hipotenusa de un triángulo si el valor de sus catetos es de 8 y 6 unidades.
3).-Si la hipotenusa de un triángulo rectángulo es de 15 unidades y uno de sus lados es de 9 unidades, determina entonces el valor de su tercer lado.
4).- Si uno de los lados de un triángulo rectángulo vale 3x y el segundo lado vale 4x, determina el valor de la hipotenusa.
5.-) El alumno podrá hacer una tabla semejante a la de los criterios de congruencia, en donde se establezcan los criterios de “semejanza entre dos triángulos”. Para ello se recomienda la visita a un faro en la dirección siguiente: http://www.rinconmatematico.com/